Strange Loop 2019 - Enhancing Angklung Music Rehearsals with Modern Tech
Overview
Angklung is a traditional musical instrument from Indonesia. This instrument has a lot of variety in how it is performed; a common format is the orchestral format in which 15-30 players gather to form a team. Playing angklung in this way is fun but also presents some challenges that are hard to solve manually. In this talk, we will learn how technology is used to improve the quality of rehearsals of this age-old instrument.
Trapsilo comes from Bandung, Indonesia. Bandung is the 3rd largest city in Indonesia.
Trapsilo has played Angklung for over 10 years and has played in Italy, Greece, Malaysia and Singapore and has also conducted several concerts and performances.
He has been programming far longer than he has been playing Angklung. Naturally he thought of programming ways to solve the problems his groups had when doing performances.
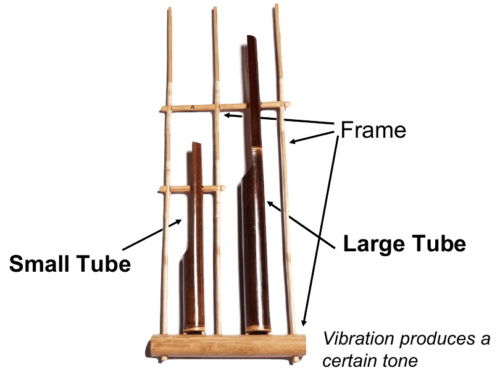
What is an Angklung?
They are made of bamboo tubes. Larger Angklung produce lower frequency notes and smaller Angklung produce higher frequency notes.
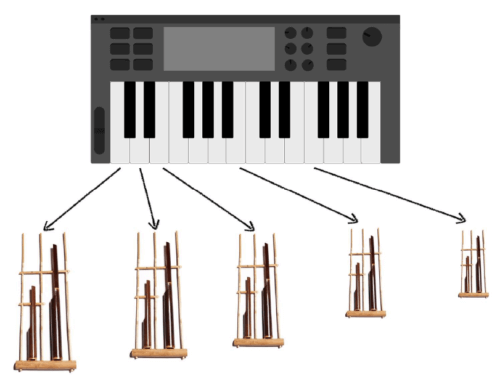
To visualize Angklung pitches look at a keyboard. Each Angklung represents one key on a piano keyboard.
How is it played?
An Angklung performance is done by many performers. Each performer plays multiple Angklung.

Angklung Cipher Notation
Traditional western music notation cannot be used. Angklung players read a Cipher Notation. It is read it left to right, top to bottom.
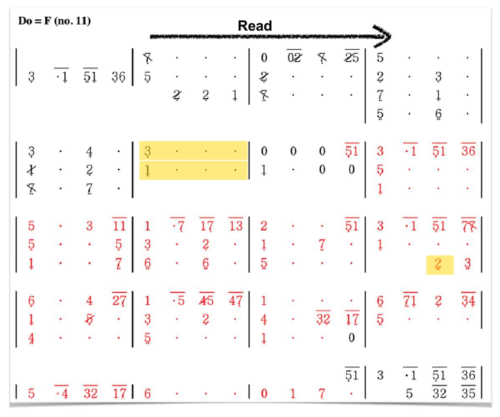
Angklung Cipher notation encodes a lot of information like key signature, octave, absolute and relative notes.
What are the difficulties of an Angklung performance?
There are more Angklung than players, so how do we distribute the Angklung among the performers?
Can We Distribute Angklung randomly?
No. There are problems with this naive approach.
Multiple Angklung are assigned to each person in order to cover all of the pitches required for a performance.
Performers cannot play two Angklung of a different pitch at the same time.
Each player will want to participate evenly. They will not want to just play one note.
A player assigned a bunch of small Angklung will have a hard time playing them. Likewise a player assigned a bunch of large Angklung will also have difficulty. The players need a good range of Angklung assigned to them.
The Solution
Let's program it.
Since this is an optimization problem, there is no one right answer. There are multiple acceptable solutions.
The Angklung Cipher notation is a table like a spreadsheet. So we can put Cipher Notation into Excel.

What kind of algorithm could help us distribute the instruments better among the performers?
Algorithm Goals
What is the optimal distribtion of Angklung among players?
- Minimize collisions (2 players can't play the same note)
- Maximize amount of player's time (don't want to leave someone out :( )
- Good balance of size of Angklungs
The Algorithm
- Read in the spreadsheet in
- Compute note collisions in the piece (build a collision table)
- Compute player time
- Compute Angklung size distribution
Use the collision table to assign a weight to the Angklung.
Decrease the weight based on the play time.
If a player already has a big Angklung, don't give that player a big one.
Do we consider the strength of the Angklung player?
Player ability is hard to quantify. Initial implementation took this into account but was later abandoned.
Implementation
Load Excel SpreadSheet
wb = openpyxl.load_workbook(file_name)
score = [] # music score, List[List[notes]]
for row in wb.active.rows:
is_empty_row = True
for cell in row:
if re.match(NOTE_VALID_CHARS, cell.value):
is_empty_row = False
new_row.append(cell.value)
if is_empty_row:
internal row = 0
score[internal_row] += new_row
internal row += 1 Calculate Collision Table
def calculate_collision_table(score):
angklung_per_column = {}
all_angklung = set()
for row in score:
for col, beat in enumerate(row):
if col not in angklung_per_column:
angklung_per_column[col] = set()
for m in re.finditer("<[0-9A-Gg#]+>", beat):
angklung = m[0].strip("<>")
angklung_per_column[col].add(angklung)
all_angklung.add(angklung)
collision_table = {}
while len(all_angklung) > 0:
a = all_angklung.pop()
for b in all_angklung:
collision_table[pair(a, b)] = 0
for i, col in angklung_per_column.items():
processing = col.copy()
while len(processing) > 0:
a = processing.pop()
for b in list(processing) + list(angklung_per_column.get(i+1, set()) - {a}):
collision_table[pair(a, b)] += 1
# normalize
max_collision = (len(score) * 2) - 1
norm_collision_table = {}
for a_pair in collision table:
norm_collision_table[a_pair] = collision_table[a_pair] / max_collision
return norm_collision_table Calculate Play Time
def calculate_play_time(*partiturs):
play_time = {}
for row in score:
joined_row = ''.join(row)
for m in re.finditer(r'(-|-=)?(<[4A-Gg0-9#]{1,2}>)((?:(?:-|-=)?\.+)*)', joined_row):
if m[1] == '-':
duration = 0.5
elif m[1] '-=':
duration = 0.25
else:
duration = 1
for m2 in re.finditer(r'(-|-=)?\.', m[3]):
if m2[1] == '-':
duration += 0.5
elif m2[1] == '-=':
duration += 0.25
else: duration += 1
angklung = m[2].strip('<>')
try:
play_time[angklung] += duration
except KeyError:
play_time[angklung] = duration
# normalize
total_len_partiturs = sum(len(partitur) for partitur in partiturs)
norm_play_time = {}
for no_angklung in play_time:
norm_play_time[no_angklung] = play_time[no_angklung] / total_len_partiturs
return norm_play_time Calculate Instrument Distribution
def generate_distribution(play_time, collision_table, num_players, num_each_angklung):
angklung_to_distribute = []
for a, j in num_each_angklung.items():
angklung_to_distribute.extend(a for _ in range(j)])
random.shuffle(angklung_to_distribute)
distribution = {i: [] for i in range(num_players)}
while len(angklung_to_distribute) > 0:
angklung_candidate = angklung_to_distribute.pop()
candidate_values = {}
for player_index, player_distribution in distribution.items():
if angklung_candidate in player_distribution:
continue
weight = 0
for players_angklung in player_distribution:
weight -= play_time[players_angklung]
weight -= collision_table[pair(angklung_candidate, players_angklung)]
if angklung_candidate LOW_ANGKLUNG and \
players_angklung it LOW_ANGKLUNG:
weight -= 1
weight -= 1 / abs(no_angklung_to_numeral(angklung_candidate)
- no_angklung_to_numeral(players_angklung))
weight -= len(player_distribution) * 3
candidate_values[player_index] = weight
if len(candidate_values) == 0:
raise Exception("Too few players")
candidate_values_sorted = sorted([(v, i) for i, v in candidate_values.items()],
key=lambda t: t[0], reverse=True)
distribution[candidate_values_sorted[0][1]].append(angklung_candidate)
distribution = {i: sorted(angklungs, key=no_angklung_to_numeral)
for i, angklungs in distribution.items()}
return distribution